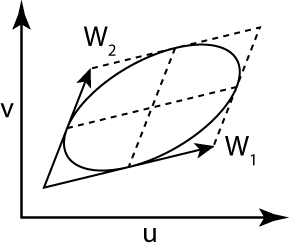
The Ptex filter footprint is specified as two vectors in uv space:

\[ W_1 = [uw1, vw1] \\ W_2 = [uw2, vw2] \]

The vectors form a parallelogram around the sample point, \( [u, v] \).

When the vectors are orthogonal, they form the major and minor axis of the enclosed ellipse.

Determining the filter footprint

In general, the vectors represent the uv sampling interval along two axes, a and b:

\[ [uw1, vw1] = \left[ \frac{du}{da}, \frac{dv}{da} \right] \\ [uw2, vw2] = \left[ \frac{du}{db}, \frac{dv}{db} \right] \]

Two special cases are of interest:

A) Texture aligned grid (the classic Ptex case) - the vectors form two sides of a rectangle, uw by vw:

\[ [uw1, vw1] = [uw, 0] \\ [uw2, vw2] = [0, vw] \]

B) Projection from screen space (where a and b are screen coordinates in pixels):

Given derivatives of the screen coordinates:

\[ \frac{da}{du} = Du(a) \]

\[ \frac{db}{du} = Du(b) \]

\[ \frac{da}{dv} = Dv(a) \]

\[ \frac{db}{dv} = Dv(b) \]

the vectors can be found by inverting the Jacobian matrix \( \begin{bmatrix} \frac{da}{du} & \frac{db}{du} \\ \frac{da}{dv} & \frac{db}{dv} \end{bmatrix} \):

\[ det = \left( \frac{da}{du} * \frac{db}{dv} - \frac{db}{du} * \frac{da}{dv} \right) \]

\[ \frac{du}{da} = \frac{1}{det} * \frac{db}{dv} \]

\[ \frac{dv}{da} = -\frac{1}{det} * \frac{db}{du} \]

\[ \frac{du}{db} = -\frac{1}{det} * \frac{da}{dv} \]

\[ \frac{dv}{db} = \frac{1}{det} * \frac{da}{du} \]

\[ [uw1, vw1] = \left[ \frac{du}{da}, \frac{dv}{da} \right] \\ [uw2, vw2] = \left[ \frac{du}{db}, \frac{dv}{db} \right] \]

Note: if the ptex u, v coordinates aren't aligned with the renderer's uv coordinates, the chain rule can be used.

Given texture coordinates s and t:

\[ \frac{ds}{du} = Du(s) \]

\[ \frac{dt}{du} = Du(t) \]

\[ \frac{ds}{dv} = Dv(s) \]

\[ \frac{dt}{dv} = Dv(t) \]

\[ [uw1, vw1] = \left[ \frac{ds}{du} * \frac{du}{da} + \frac{ds}{dv} * \frac{dv}{da}, \frac{dt}{du} * \frac{du}{da} + \frac{dt}{dv} * \frac{dv}{da} \right] \]

\[ [uw2, vw2] = \left[ \frac{ds}{du} * \frac{du}{db} + \frac{ds}{dv} * \frac{dv}{db}, \frac{dt}{du} * \frac{du}{db} + \frac{dt}{dv} * \frac{dv}{db} \right] \]